一、对称

感谢AJ-GK老师为本章提供大部分素材，感兴趣的小伙伴可以b站或者小红书搜索 AJ-GK 了解更多

图推-对称思维：遇到对称类的题目，优先考虑对称轴数量角度和图形点线面的数量/位置关系，及内外图形对称轴等

1.轴对称

1）判定：图形沿某条直线（即对称轴）对折后完全重合。

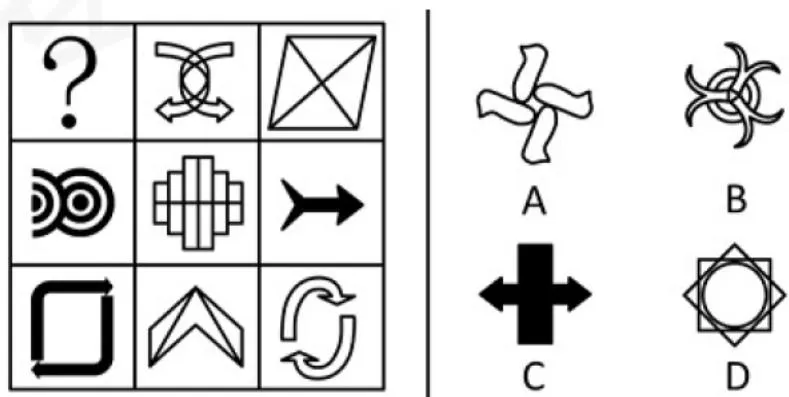
图形均为轴对称图形，答案为 C

2）常考方式：

1. 轴对称判定（如等腰三角形、箭头形）。

2. 对称轴特性（如轴的方向、数量等）。

3. 复合其他考点（如中心对称等）

3）易错点：

1. 忽略非竖直/水平对称轴（如斜向对称轴） 2.忽略非整体对称（即部分对称：如图25国考）

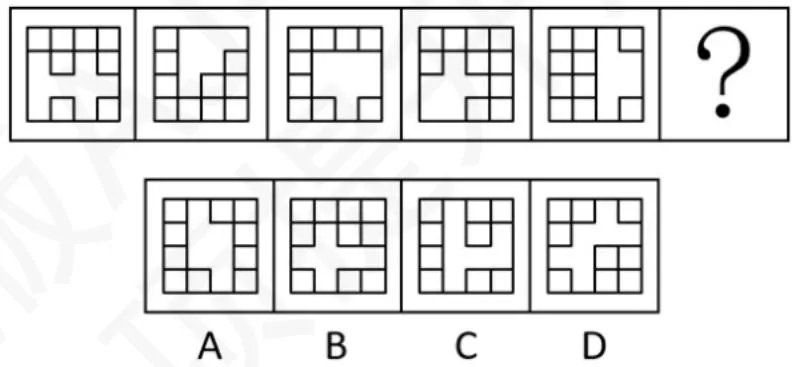
观察图片中的空白区域，均为对称图形且对称轴依次顺时针旋转 45度，故答案选 D

2. 中心对称

1）判定：绕中心旋转 $180^{\circ}$ 后与原图重合，如S形、Z形、平行四边形。

2）常考方式：

1. 单独考查中心对称图形分类。

134为中心对称，256 为轴对称

2. 组合图形中某部分为中心对称（如内部元素旋转 $180^{\circ}$ ）。

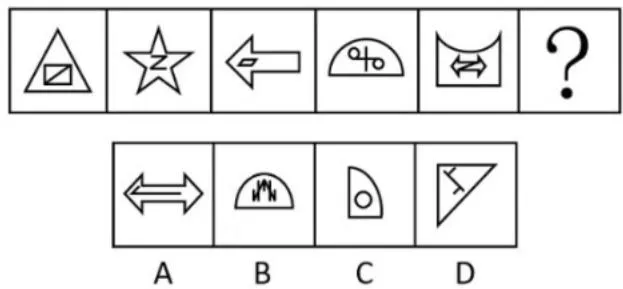
图形分开考虑，外部轮廓为轴对称，内部元素为中心对称，故答案选 D

3）易错点：

1. 混淆轴对称与中心对称（如误判五角星为中心对称）。
2. 忽略局部中心对称（如隐藏的旋转元素）。

3.轴对称 + 中心对称

1）判定：同时满足轴对称和中心对称（有两条互相垂直的对称轴），如正方形等。

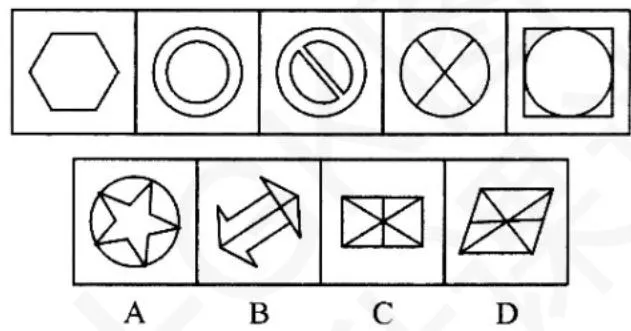
图形均为轴对称+中心对称图形，故答案选择 C

2）常考方式：

1. 对称轴数量为偶数（如矩形2条、正六边形6条）。

2. 分组分类（如 $①③⑥$ 为轴对称 + 中心对称， $②④⑤$ 仅轴对称）。

3）易错点：

知识点不牢固导致误判图形同时具备两种对称性。

4.对称轴方向

1）常考方式：

1. 对称轴方向一致（如所有图形均为竖直对称轴）。

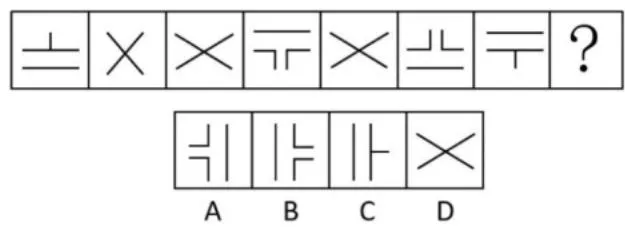
题目中的图形均有对称轴且为垂直方向的对称轴，故答案选 D

2. 对称轴方向旋转（如25浙江：对称轴依次顺时针旋转 $45^{\circ}$ ）。

图片中的对称轴按顺时针依次旋转 45度，故答案选择 D

2）易错点：

1. 未注意斜向对称轴的方向（如 $45^{\circ}$ ， $30^{\circ}$ ）； 2. 借助黑白块考察对称（黑白块模块会讲到）

5.对称轴数量

1）常考方式：

1. 数量恒定/递增/递减（如25江苏：对称轴数量递减）。

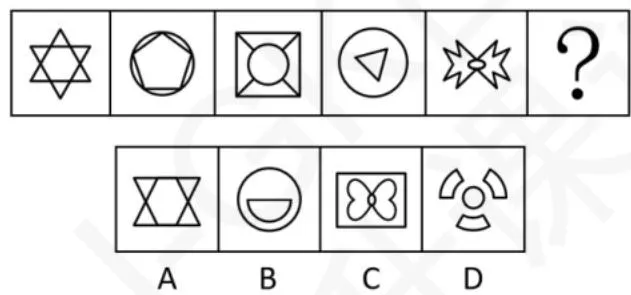
对称轴的数量依次为 6,5,4,3,2,1答案为 B

2. 分组分类（如 $③④⑥$ 有1条， $①②⑤$ 有3条）。

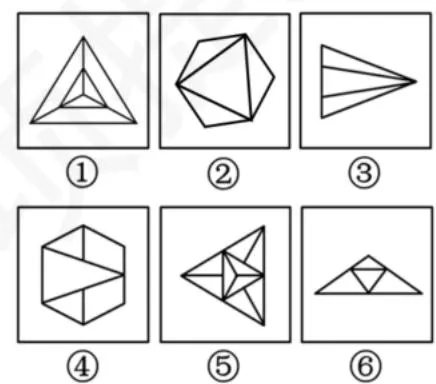
③④⑥ 有1条对称轴，①②⑤ 有3条对称轴

2）易错点：

误判复杂图形的对称轴（如嵌套图形）。

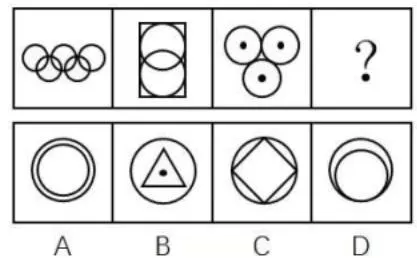
对称轴的数量依次递增分别为 1，2,3,4，故答案为 C

6.对称轴过点/线/面

1）常考方式：

1. 过点：对称轴穿过图形的顶点、中点或交点。

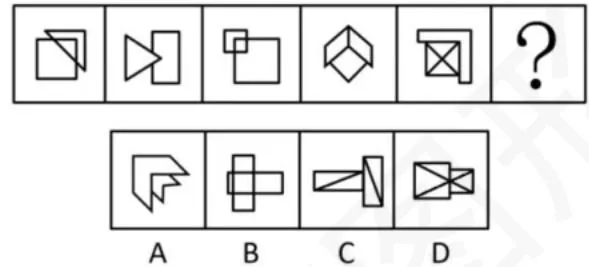
图形中均有一条对称轴，排除 C，且对称轴按顺时针旋转 45度，排除 A，对称轴均会过图形的一个交点，排除 B，选择 D

2. 过线：对称轴与图形内部线条重合。

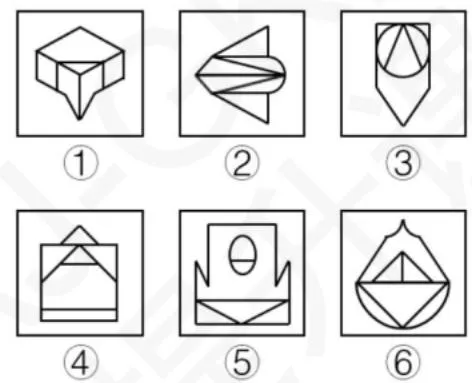
124对称轴与图形的某一条直线重合，356 对称轴与图形直线不重合

3. 过面：对称轴穿过封闭面。

156对称轴穿过图像所有平面，234 对称轴只穿过一个平面

2）易错点：

1. 忽略对称轴与图形元素的关联。
2. 结合其他考点（如对称轴数量+过点线面）综合考查。

7.两条对称轴关系

1）判定：图形由两个小轴对称图形组成（如25联考：每图均有一黑一白两个小轴对称图形，并且两对称轴依次垂直/平行交替）

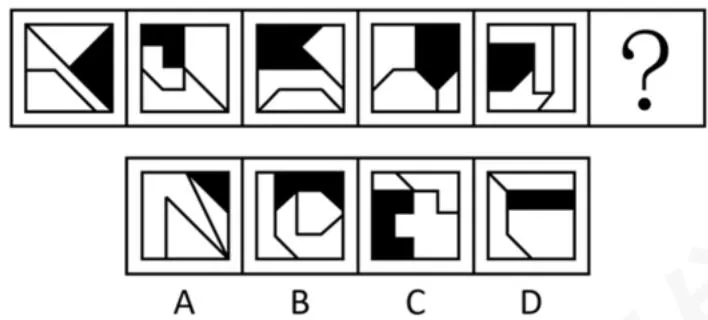
黑色图形与图形中唯一白色轴对称图形的对称轴分别呈现垂直、平行、垂直、平行的交替出现的关系，且黑色图形只有一条对称轴，所以选 A

2）常考方式：

对称轴垂直或对称轴夹角固定（如 $60^{\circ}$ ， $45^{\circ}$ )，对称轴夹角递增（ $30^{\circ}\rightarrow 60^{\circ}\rightarrow 90^{\circ}$ ）。

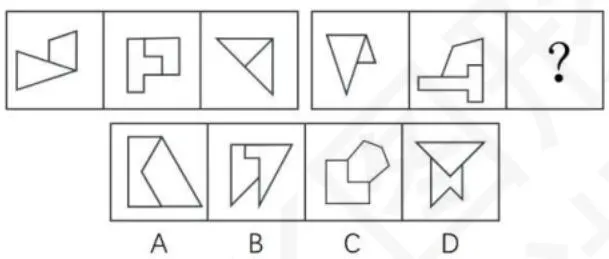
将图形分开考虑，两个子图形对称轴分别呈现平行（0 度）、夹角 45度， 垂直（夹角 90度）的关系，故答案选 D（垂直）

3）新考法：嵌套对称（如25湖北选调：每图外框为轴对称图形，并且均有一个轴对称的面，其两条对称轴的关系为平行、垂直交替）

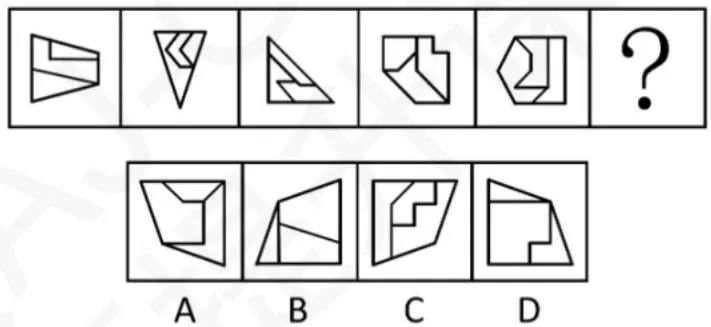
外轮廓图形和内部子图形的对称轴分别呈现平行、垂直的交替出现的关系，故答案选 D

3）易错点：

小轴对称图形的识别与判定不熟练。

拓展：“米”字规律

🎯 扫码练一练

AI刷题，天下无敌；上岸在手，编制我有！

🤖 上岸小助手

• 24小时在线答疑
• 个性化学习指导
• 最新考试资讯