数量关系
数量模版题
平面几何

数量关系第十二课：平面几何

一、基础公式

常用周长公式

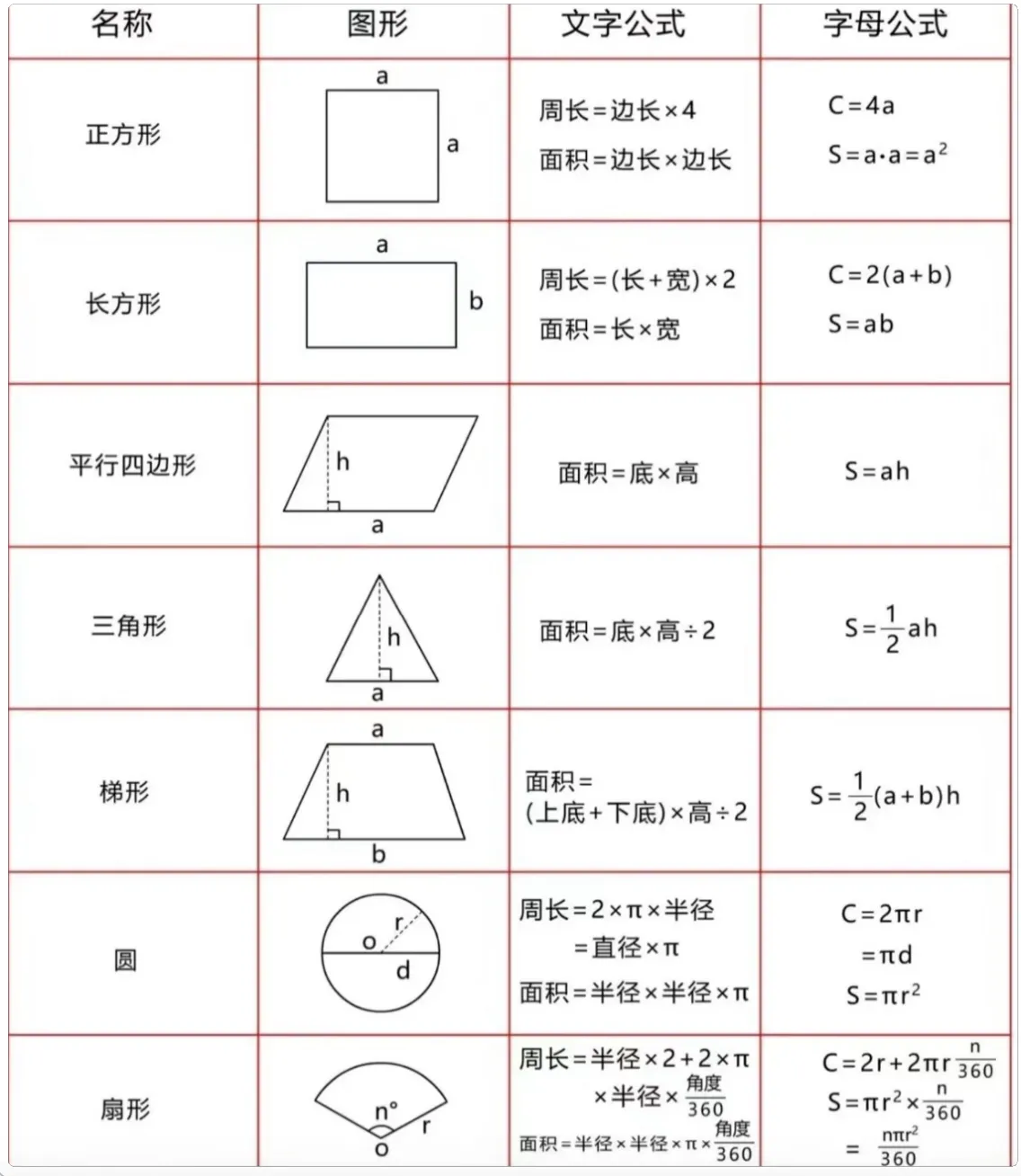
image1 image2

图形图示周长面积
正方形a4aS=a2S = a^2
长方形a2(a+b)S=abS = ab
三角形ca+b+cS=12ahS = \frac{1}{2}ah
正三角形a3aS=34a2S = \frac{\sqrt{3}}{4} a^2
圆形(a)2πr2\pi rS=πr2S = \pi r^2
扇形(n°)弧长 = n360×2πr\frac{n}{360} \times 2\pi rS=n360×πr2=lr2S = \frac{n}{360} \times \pi r^2 = \frac{lr}{2}
梯形ba+b+c+dS=(上底+下底)×高2S = \frac{(\text{上底}+\text{下底}) \times \text{高}}{2}
平行四边形a2a+2bS=ahS = ah
菱形A4aS=对角线×对角线2S = \frac{\text{对角线} \times \text{对角线}}{2}

几何最值理论

1、立体最值

（1）立体图形中，若表面积一定，越接近于球，体积越大。 （2）立体图形中，若体积一定，越接近于球，表面积越小。

2、平面最值

（1）平面图形中，周长一定，越接近于圆，面积越大； （2）平面图形中，面积一定，越接近于圆，周长越小。

长方形最值（特殊矩形）

（1）四边形周长一定时，正方形面积最大。 （2）四边形面积一定时，正方形周长最小。

常用角度关系

  • 三角形内角和 = 180°
  • n边形内角和 = (n−2)×180°(n-2) \times 180°
  • 圆心角 = 2×2 \times 圆周角
  • 过直径圆周角 = 90°

正余弦函数

基本关系：

  • sin⁡A=对边斜边\sin A = \frac{\text{对边}}{\text{斜边}}
  • cos⁡A=邻边斜边\cos A = \frac{\text{邻边}}{\text{斜边}}
  • tan⁡A=对边邻边=sin⁡Acos⁡A\tan A = \frac{\text{对边}}{\text{邻边}} = \frac{\sin A}{\cos A}
  • sin⁡A=cos⁡(90°−A)=sin⁡(180°−A)\sin A = \cos(90°-A) = \sin(180°-A)

特殊角度值：

角度sin⁡\sincos⁡\costan⁡\tan
30°12\frac{1}{2}32\frac{\sqrt{3}}{2}33\frac{\sqrt{3}}{3}
45°22\frac{\sqrt{2}}{2}22\frac{\sqrt{2}}{2}1
60°32\frac{\sqrt{3}}{2}12\frac{1}{2}3\sqrt{3}
15°6−24\frac{\sqrt{6}-\sqrt{2}}{4}6+24\frac{\sqrt{6}+\sqrt{2}}{4}2−32-\sqrt{3}

三角形常见比例关系

勾股定理： a2+b2=c2a^2 + b^2 = c^2

常用勾股数：

  • 3、4、5
  • 5、12、13
  • 8、15、17
  • 7、24、25

特殊三角形边长比例：

  • 30°直角三角形 = 1:3:21 : \sqrt{3} : 2
  • 45°等腰直角三角形 = 1:1:21 : 1 : \sqrt{2}
  • 120°等腰三角形 = 1:1:31 : 1 : \sqrt{3}

直角三角形中线长度：

  • 中线长度 = 12×\frac{1}{2} \times 斜边长
  • 30°直角三角形中，中线长度 = 短直角边长

二、距离型问题

勾股定理应用

例题1：半圆游泳池问题

题目：如下图所示，甲和乙在面积为 54π54\pi 的半圆形游泳池内游泳，他们分别从位置A和B同时出发，沿直线同时游到位置C。若甲的速度为乙的2倍，则原来甲、乙两人相距：

选项：

  • A. 9
  • B. 15
  • C. 9
  • D. 18

解析：

因为AC是直径，所以 ∠ABC=90°\angle ABC = 90°。

半圆面积是 54π54\pi，所以 12πr2=54π\frac{1}{2}\pi r^2 = 54\pi，所以 r=63r = 6\sqrt{3}，所以 AC=123AC = 12\sqrt{3}。

因为甲速度是乙的2倍，耗时相同，所以 AC=2BCAC = 2BC，sin⁡∠BAC=12\sin \angle BAC = \frac{1}{2}，所以 ∠BAC=30°\angle BAC = 30°。

所以 AB=123×32=18AB = 12\sqrt{3} \times \frac{\sqrt{3}}{2} = 18，选择D选项。

三角形相似

例题2：光影相似问题

题目：楼道上方有一盏灯，小刘径直走向这盏灯。一开始，他发现自己影子的长度为3.2米，前进1米后，发现影子缩短为1.6米。已知小刘身高为1.6米，则这盏灯的高度约为（）米。

选项：

  • A. 2.6
  • B. 2.8
  • C. 3.2
  • D. 3.4

解析：

移动形成两次光影平行相似是行测中比较经典的相似问题，核心思想在于用两次相似表示出两组相似三角形的交叉部分EB的长度，建立等量关系从而求解x。

因为 AB∥COAB \parallel CO，BD=2ABBD = 2AB，所以 DO=2CO=2xDO = 2CO = 2x

因为 AB1∥COAB_1 \parallel CO，AB1=B1E=1.6AB_1 = B_1E = 1.6，所以 EO=CO=xEO = CO = x，所以 ED=2x−x=xED = 2x - x = x

EB=BD−ED=3.2−xEB = BD - ED = 3.2 - x，EB=EB1−BB1=1.6−1=0.6EB = EB_1 - BB_1 = 1.6 - 1 = 0.6

所以 3.2−x=0.63.2 - x = 0.6，x=2.6x = 2.6，所以选择A选项。

例题3：梅涅劳斯定理应用

题目：某社区进行更新改造，要在雨季前完成社区内一条主干道AC的维修。在BC路段设置临时通道分流点D，BD：DC=2：1；在AD路段设置指挥点E，AE：ED=1：2。若从社区服务中心B经指挥点E向主干道AC引一条物资运输线与AC交于F点，则AF段与FC段的长度之比是（）。

选项：

  • A. 1:2
  • B. 1:3
  • C. 1:4
  • D. 1:5

解析：

方法一：过D点作AC平行线交BF于G。

因为 DG∥FCDG \parallel FC，所以 △ABG∼△BFC\triangle ABG \sim \triangle BFC，所以 DG:FC=BD:BC=2:3DG : FC = BD : BC = 2 : 3。

又因为 DG∥AFDG \parallel AF，所以 △EGD∼△EFA\triangle EGD \sim \triangle EFA，所以 AF:DG=AE:ED=1:2AF : DG = AE : ED = 1 : 2。

AF:DG=1:2AF : DG = 1 : 2，DG:FC=2:3DG : FC = 2 : 3，所以 AF:FC=1:3AF : FC = 1 : 3，选择B。

方法二：根据梅涅劳斯定理，BF与△ACD的三条边分别交于F、E、B，所以：

AEED×DBBC×CFFA=1\frac{AE}{ED} \times \frac{DB}{BC} \times \frac{CF}{FA} = 1

所以 12×23×CFFA=1\frac{1}{2} \times \frac{2}{3} \times \frac{CF}{FA} = 1，所以 AF:FC=1:3AF : FC = 1 : 3，选择B选项。

射影定理

射影定理公式：

  1. AD2=BD×DCAD^2 = BD \times DC
  2. AB2=BD×BCAB^2 = BD \times BC
  3. AC2=CD×BCAC^2 = CD \times BC

证明：通过相似三角形关系可证。

例题4：射影定理应用

题目：一块长方形土地ABCD中绘有3条测绘线如图所示。已知AE和CF垂直于对角线BD，AE、EF分别长8米和12米。问整块土地的面积为多少平方米？

选项：

  • A. 96
  • B. 156
  • C. 160
  • D. 240

解析：

因为 ∠BAD=90°\angle BAD = 90°，AE⊥BDAE \perp BD，所以 AE2=BE×EDAE^2 = BE \times ED

假设 BE=aBE = a，则 82=a×(12+a)8^2 = a \times (12 + a)，即 64=12a+a264 = 12a + a^2，解得 a=4a = 4

所以 BD=BE+EF+FD=4+12+4=20BD = BE + EF + FD = 4 + 12 + 4 = 20米

所以三角形ABD面积 = 12×BD×AE=12×20×8=80\frac{1}{2} \times BD \times AE = \frac{1}{2} \times 20 \times 8 = 80平方米

所以整块土地面积 = 2×S△ABD=2×80=1602 \times S_{\triangle ABD} = 2 \times 80 = 160平方米，选择C。

将军饮马问题

原理：两定点 + 动点，利用对称令动点位于顶点之间。

例题5：将军饮马经典问题

题目：A、B 两村在一条笔直公路的同侧，到公路的垂直距离分别是 3 公里和 7 公里，两村相距 8.5 公里，现需在公路边建一个物资集散中心，为节约物资配送成本，集散中心到两个村的直线路程之和应尽可能小，若货车的速度约为 60 公里/小时，那么货车从集散中心出发，到两村送货后返回中心，路途所花费的最少时间为：

选项：

  • A. 18分钟
  • B. 21分钟
  • C. 24分钟
  • D. 27分钟

解析：

以公路MN作A点镜像对称点A1A_1、B点镜像对称点B1B_1，则 AO+BO=A1O+BOAO + BO = A_1O + BO，所以当 A1O+BOA_1O + BO 最小时，总路程 AO+BO+ABAO + BO + AB 有最小值。

两点之间直线最短，所以当O就在 A1BA_1B 与MN交点上时，距离最短。

BB1=BN+NB1=BN+MA1=BN+AM=7+3=10BB_1 = BN + NB_1 = BN + MA_1 = BN + AM = 7 + 3 = 10km

A1B1=ADA_1B_1 = AD，而AD、BD（4）、AB（8.5）构成直角三角形，注意到4与8.5比值为8：17，考虑勾股数8、15、17，所以 AD=152=7.5AD = \frac{15}{2} = 7.5，所以 A1B1=7.5A_1B_1 = 7.5

所以 A1B2=7.52+102=56.25+100=156.25=12.52A_1B^2 = 7.5^2 + 10^2 = 56.25 + 100 = 156.25 = 12.5^2（3、4、5勾股数比例关系），所以 A1B=12.5A_1B = 12.5km

所以最短总路程 = 12.5+8.5=2112.5 + 8.5 = 21km，需要 2160\frac{21}{60}h，即21分钟，所以选择B。

线圆相切问题

原理：切点、切线是从一个点"绕过"圆的最短路径。

例题6：线圆相切应用

题目：A、B两地分别与某个半径150米的圆形池塘边缘相距100米、AB的连线经过池塘的圆心，张某从A地出发以1米/秒的速度匀速行走。全程除转向1次外均保持直线行进。问他从A地到B地的最短用时在以下哪个范围内？

选项：

  • A. 不到9分30秒
  • B. 9分30秒—10分之间
  • C. 10分—10分30秒之间
  • D. 10分30秒以上

解析：

因为只转弯一次，其余都是直线，所以张某的路径为两条直线，想要距离最短，就要尽量贴着圆形的池塘，所以会和池塘相切。

过A、B做切线切于D、E两点，交于C点。所以 OD⊥ACOD \perp AC，OE⊥BCOE \perp BC，所以 AD2=AO2−OD2=2502−1502=62500−22500=40000=2002AD^2 = AO^2 - OD^2 = 250^2 - 150^2 = 62500 - 22500 = 40000 = 200^2，AD=200AD = 200，同理 BE=200BE = 200。

因为 △AOC\triangle AOC 和 △AOD\triangle AOD 都是直角三角形，且共角A，所以 △AOC\triangle AOC 和 △AOD\triangle AOD 相似，所以 AD:OD=OD:DCAD : OD = OD : DC，所以 DC=OD2AD=1502200=22500200=112.5DC = \frac{OD^2}{AD} = \frac{150^2}{200} = \frac{22500}{200} = 112.5，所以 AC=BC=AD+DC=200+112.5=312.5AC = BC = AD + DC = 200 + 112.5 = 312.5

所以总路程为 AC+BC=312.5+312.5=625AC + BC = 312.5 + 312.5 = 625米，所以用时 = 6251=625\frac{625}{1} = 625秒 = 10分25秒，选择C选项。

三、面积型问题

基础运算

例题7：周长与面积转换

题目：一根绳子，把它围成一个长度是宽度的两倍的长方形时，面积是32平方厘米，如果把它围成一个等边三角形，面积是多少平方厘米。

选项：

  • A. 32332\sqrt{3}
  • B. 24324\sqrt{3}
  • C. 18318\sqrt{3}
  • D. 16316\sqrt{3}

解析：

长方形面积 = ab=2b×b=2b2=32cm2ab = 2b \times b = 2b^2 = 32cm^2，解得 b2=16b^2 = 16，b=4cmb = 4cm，a=2b=8cma = 2b = 8cm。

所以绳子长度 = 长方形周长 = 2(a+b)=2×(8+4)=2×12=24cm2(a + b) = 2 \times (8 + 4) = 2 \times 12 = 24cm。

所以等边三角形边长 = 243=8cm\frac{24}{3} = 8cm，面积 = 34×a2=34×82=34×64=163cm2\frac{\sqrt{3}}{4} \times a^2 = \frac{\sqrt{3}}{4} \times 8^2 = \frac{\sqrt{3}}{4} \times 64 = 16\sqrt{3}cm^2，所以选择D。

拉窗帘原理

原理：三角形面积 = 12ah\frac{1}{2}ah，平行线之间距离相等。

例题8：拉窗帘应用

题目：如下图所示, 在三角形工地 ABC 中 CD=3AD, EC=2BE, 阴影部分三角形 ADE 的面积是 15 平方米。三角形工地 ABC 的面积是 ( ) 平方米?

选项：

  • A. 90
  • B. 70
  • C. 60
  • D. 45

解析：

取 EE′∥ACEE' \parallel AC 交AB于E′E', 又因为 EC=2BEEC = 2BE, 所以 AE′=2BE′AE' = 2BE', 即 AE′=23ABAE' = \frac{2}{3} AB。

因为 CD=3ADCD = 3AD，所以 AD=14ACAD = \frac{1}{4} AC，所以 S△ADE′=ADAC×AE′AB×S△ABC=14×23×S△ABC=16S△ABCS_{\triangle ADE'} = \frac{AD}{AC} \times \frac{AE'}{AB} \times S_{\triangle ABC} = \frac{1}{4} \times \frac{2}{3} \times S_{\triangle ABC} = \frac{1}{6} S_{\triangle ABC}

又因为 EE′∥ACEE' \parallel AC，所以 S△ADE=S△ADE′S_{\triangle ADE} = S_{\triangle ADE'}

而 S△ADE=15S_{\triangle ADE} = 15平方米, 所以 S△ABC=15×6=90S_{\triangle ABC} = 15 \times 6 = 90平方米。选择A选项。

正弦定理

正弦定理面积公式：三角形面积 = 12absin⁡C\frac{1}{2}ab\sin C

原理：2个三角形如果有相同角或者互补角, 则面积比 = 夹边乘积比

例题9：相同角面积比

题目：如图 ABCD 是一个梯形, E 是 AD 的中点, 直线 CE 把梯形分成甲、乙两部分, 其面积之比是 15:7 。问上底 AB 与下底 CD 的长度之比是:

选项：

  • A. 5:7
  • B. 6:7
  • C. 4:7
  • D. 3:7

解析：

赋值 S△EDC=7S_{\triangle EDC} = 7，连接AC，因为E是AD中点，所以 S△AEC=S△EDC=7S_{\triangle AEC} = S_{\triangle EDC} = 7，所以 S△ABC=15−7=8S_{\triangle ABC} = 15 - 7 = 8。

因为 AB∥CDAB \parallel CD，所以 ∠BAC=∠ACD\angle BAC = \angle ACD，且△ABC\triangle ABC与△ACD\triangle ACD共边AC，所以 S△ABC:S△ACD=AB:CD=8:(7+7)=4:7S_{\triangle ABC}:S_{\triangle ACD} = AB:CD = 8:(7 + 7) = 4:7，所以选择C。

和定积最

原理：矩形周长不变，越接近正方形，面积越大；若矩形面积不变，越接近正方形，周长越小。

引申：

  • 平面图形中，若周长不变，越接近圆，面积越大
  • 平面图形中，若面积不变，越接近圆，周长越小
  • 立体图形中，若表面积不变，越接近球体，体积越大
  • 立体图形中，若体积不变，越接近球体，表面积越小

例题10：和定积最应用

题目：某健身馆准备将一块周长为100米的长方形区域划为瑜伽场地，将一块周长为160米的长方形区域划为游泳场馆，若瑜伽场地和游泳场馆均是满足周长条件下的最大面积，问两块场地面积之差为多少平方米？

选项：

  • A. 625
  • B. 845
  • C. 975
  • D. 1150

解析：

长方形周长不变的情况下，正方形面积最大，所以瑜伽场地最大面积为 (100/4)2=252=625(100/4)^2 = 25^2 = 625平方米，游泳场馆最大面积为 (160/4)2=402=1600(160/4)^2 = 40^2 = 1600平方米，所以两块场地面积之差为 1600−625=9751600 - 625 = 975平方米，选择C。

蝴蝶定理

蝴蝶定理：任意四边形对角线连接形成四个部分，对角部分面积乘积相等。

S1×S3=S2×S4S_1 \times S_3 = S_2 \times S_4

如果四边形是梯形或者平行四边形，存在平行线，则 S2=S4=S1×S3S_2 = S_4 = \sqrt{S_1 \times S_3}

常用蝴蝶比例关系：

  • 上下底边长度比 1:21:2，四部分面积比为：1:2:2:41:2:2:4
  • 上下底边长度比 1:31:3，四部分面积比为：1:3:3:91:3:3:9
  • 上下底边长度比 2:32:3，四部分面积比为：4:6:6:94:6:6:9

例题11：蝴蝶定理应用

题目：一块种植花卉的矩形土地如图所示，AD 边长是 AB 的 2 倍，E 是 CD 的中点，甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。则种植白花的面积占矩形土地面积的：

选项：

  • A. 34\frac{3}{4}
  • B. 23\frac{2}{3}
  • C. 712\frac{7}{12}
  • D. 12\frac{1}{2}

解析：

根据蝴蝶定理，丙乙丁甲面积比为 1:2:2:41:2:2:4。

又：△BDE\triangle BDE 与 △BEC\triangle BEC 的底 DE=ECDE = EC，共高，所以 戊 = 丙 + 丁

丙乙丁甲戊面积比为 1:2:2:4:31:2:2:4:3

白花区域甲 + 戊占比为 4+31+2+2+4+3=712\frac{4 + 3}{1 + 2 + 2 + 4 + 3} = \frac{7}{12}，选择C。

面积割补

原理：不规则图形切割或者填补成规则图形计算面积。

例题12：面积割补应用

题目：如图所示, 一个小区的道路围成了一个五边形, 经实地勘测, 五边形内有三个角为直角, AD 边、BC 边和 CD 边长度相等, 且 OA 边长度为其一半。已知 AD 边长 20 米。问道路围成的五边形面积为多少平方米?

选项：

  • A. 502+20050\sqrt{2} + 200
  • B. 503+20050\sqrt{3} + 200
  • C. 502+40050\sqrt{2} + 400
  • D. 503+40050\sqrt{3} + 400

解析：

不规则图形切割为规则图形计算面积。连接 AB 得到三角形 OAB 与正方形 ABCD, 分别计算两者面积。

∵ OA=12ABOA = \frac{1}{2} AB, ∠AOB=90°\angle AOB = 90°，可以看出三角形OAB是 30° 直角三角形，OB=3OA=32AB=32AD=103mOB = \sqrt{3} OA = \frac{\sqrt{3}}{2} AB = \frac{\sqrt{3}}{2} AD = 10\sqrt{3}m

S△OAB=12×OA×OB=12×10×103=503m2S_{\triangle OAB} = \frac{1}{2} \times OA \times OB = \frac{1}{2} \times 10 \times 10\sqrt{3} = 50\sqrt{3}m^2

又 ∵ SABCD=20×20=400m2S_{ABCD} = 20 \times 20 = 400m^2

五边形面积 = 503+400m250\sqrt{3} + 400m^2，选择D。

圆相交叶子模型

叶子模型公式：

12S叶子=S扇形OAB−S三角形OAB\frac{1}{2} S_{叶子} = S_{扇形OAB} - S_{三角形OAB}

例题13：叶子模型应用

题目：下图中, 阴影部分的面积大还是条纹部分的面积大?

选项：

  • A. 阴影部分面积大
  • B. 条纹部分面积大
  • C. 两个部分一样大
  • D. 无法确定

解析：

12S叶子=S扇形OAB−S三角形OAB\frac{1}{2} S_{叶子} = S_{扇形OAB} - S_{三角形OAB}，所以条纹部分面积 = 4×S叶子=8×(S扇形OAB−S三角形OAB)=2×S大圆−4×OA24 \times S_{叶子} = 8 \times (S_{扇形OAB} - S_{三角形OAB}) = 2 \times S_{大圆} - 4 \times OA^2

假设 OA=1OA = 1，则小圆半径为1，大圆半径为2，大正方形边长为4。

此时 S条纹=2π−4≈2.28S_{条纹} = 2\pi - 4 \approx 2.28，S阴影=16−π×22=16−4π≈3.44S_{阴影} = 16 - \pi \times 2^2 = 16 - 4\pi \approx 3.44

所以 S阴影>S条纹S_{阴影} > S_{条纹}，选择A。

圆形面积割补技巧

技巧：π\pi 的"种族隔离"——圆、扇形的面积带π\pi，三角形面积不带π\pi。

例题14：圆形面积割补

题目：下面图形阴影部分面积是多少？

选项：

  • A. 12.5π12.5\pi
  • B. 25
  • C. 50−12.5π50-12.5\pi
  • D. 25π−5025\pi-50

解析：

S阴影=12×S大圆−(S半圆ABD+S扇形ABE−S△ABD)S_{阴影} = \frac{1}{2} \times S_{大圆} - (S_{半圆ABD} + S_{扇形ABE} - S_{\triangle ABD})

圆、扇形的面积带π\pi，三角形面积不带π\pi，可以锁定D选项。

=12×π×25+π×100×45360−12×10×10= \frac{1}{2} \times \pi \times 25 + \pi \times 100 \times \frac{45}{360} - \frac{1}{2} \times 10 \times 10

=12.5π+12.5π−50= 12.5\pi + 12.5\pi - 50

=25π−50= 25\pi - 50

所以选择D选项。

周期问题立体几何