数量关系
数量模版题
容斥问题

数量关系第七课：容斥问题

一、双集合

基本原理

容斥原理公式：

  • A∪B=A+B−A∩BA \cup B = A + B - A \cap B
  • A∩B=A+B−A∪BA \cap B = A + B - A \cup B

二、三集合

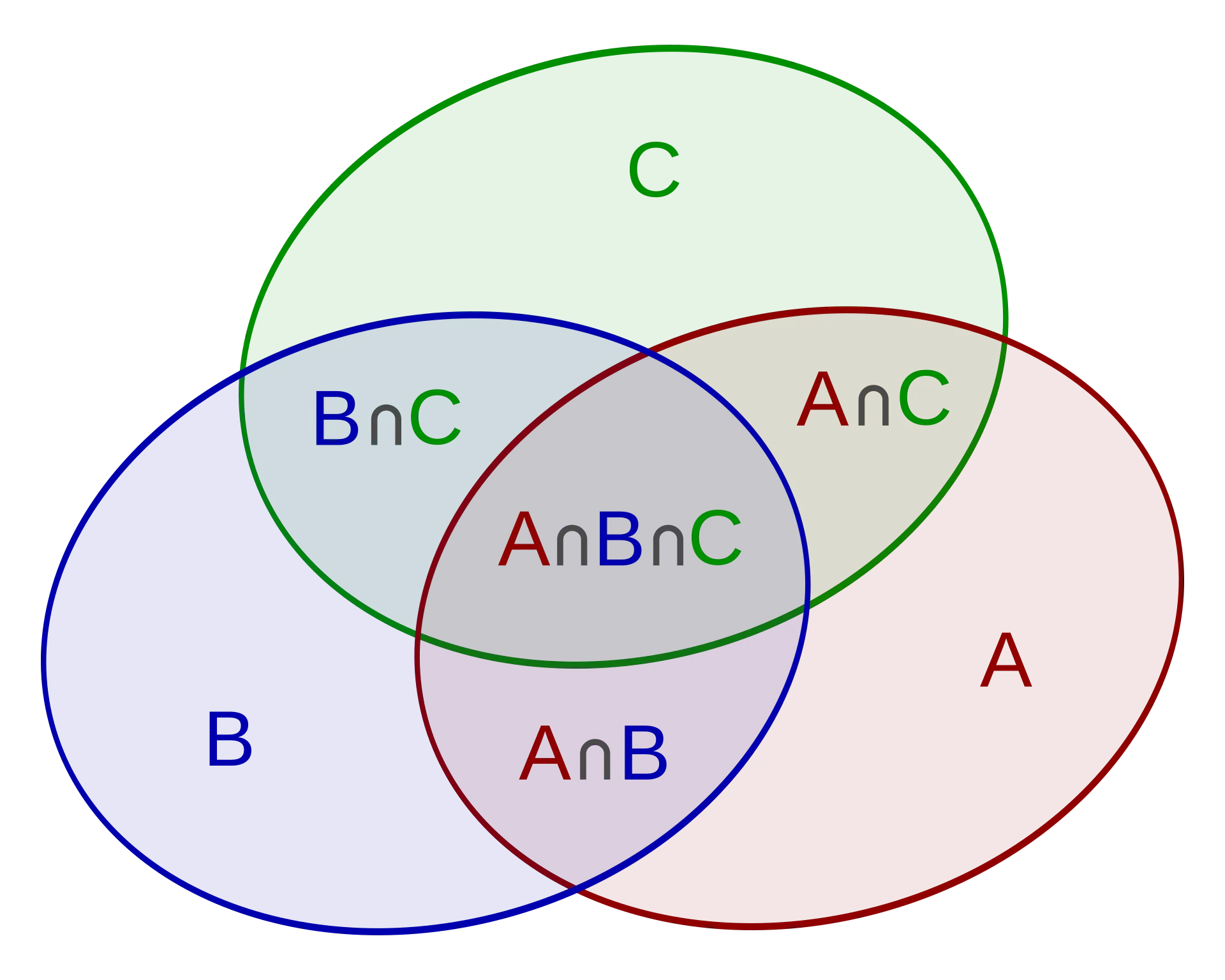
images1

1. 标准型：（动手画图）

A+B+C−A∩B−B∩C−C∩A+A∩B∩C=总−都不A + B + C - A \cap B - B \cap C - C \cap A + A \cap B \cap C = 总 - 都不

题目：（2020 新疆）某单位共有 240 名员工，其中订阅 A 期刊的有 125 人，订阅 B 期刊有 126 人，订阅 C 期刊的有 135 人，订阅 A、B 期刊的有 57 人，订阅 A、C 期刊的有 73 人，订阅 3 种期刊的有 31 人，此外，还有 17 人没有订阅这三种期刊中的任何一种。问订阅 B、C 期刊的有多少人？

  • A.57
  • B.64
  • C.69
  • D.78

解析：

直接运用标准三集合容斥公式即可 解题思路（容斥原理）

已知：总人数 240240，三者都不订阅 1717 人 ⇒∣A∪B∪C∣=240−17=223\Rightarrow |A\cup B\cup C|=240-17=223.

设 ∣B∩C∣=x|B\cap C|=x。由容斥原理： ∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣B∩C∣−∣C∩A∣+∣A∩B∩C∣|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C| 代入数据： 223=125+126+135−57−x−73+31223=125+126+135-57-x-73+31 计算： 223=287−x ⇒ x=287−223=64223=287-x\ \Rightarrow\ x=287-223=64

答案：B. 64

2. 非标准型

A+B+C−只满足两项−只满足三项×2=总−都不满足A + B + C - 只满足两项 - 只满足三项×2 = 总 - 都不满足 前提：出现只满足两个条件（注：只满足两个条件=只满足两个条件）

题目：（2019 河北）某班参加学科竞赛人数 40 人，其中参加数学竞赛的有 22 人，参加物理竞赛的有 27 人，参加化学竞赛的有 25 人，只参加两科竞赛的有 24 人，参加三科竞赛的有多少人？

  • A.2
  • B.3
  • C.5
  • D.7

解析：

已知“参加至少一科”的总人数为 40，说明“都不参加”人数为 0。代入公式：

∣A∣+∣B∣+∣C∣−只两科−2×三科=∣总∣−∣都不∣|A|+|B|+|C|-\text{只两科}-2\times\text{三科}=|\text{总}|-|\text{都不}|

即：

22+27+25−24−2x=40−022+27+25-24-2x=40-0

74−24−2x=40 ⇒ 50−2x=40 ⇒ 2x=10 ⇒ x=574-24-2x=40\ \Rightarrow\ 50-2x=40\ \Rightarrow\ 2x=10\ \Rightarrow\ x=5

答案：C. 5

扩展：N 集合容斥

images2

例题1：基础容斥应用

题目：某班有54名学生，其中有24名同学喜欢唱歌，有32名同学喜欢跳舞，唱歌、跳舞都不喜欢的有7名同学，那么既喜欢唱歌也喜欢跳舞的同学有多少人？

  • A. 9人
  • B. 23人
  • C. 28人
  • D. 13人

解析：

实际涉及到唱歌或者跳舞的学生 = 54 - 7 = 47人。

根据容斥原理：A∩B=A+B−A∪BA \cap B = A + B - A \cup B

所以同时喜欢唱歌也喜欢跳舞的同学人数 = 24 + 32 - 47 = 9人

答案：A

例题2：容斥原理应用

题目：某班共有46人参加了一次数学测验，其中35人做对了第一题，28人做对了第二题，有3人都做错了这两道题，那么该班有多少人只做对了第二题？

  • A. 8人
  • B. 11人
  • C. 15人
  • D. 18人

解析：

实际涉及到做对第一题或者第二题的学生 = 46 - 3 = 43人

所以这两题都做对的人数 = 35 + 28 - 43 = 20人

所以只做对第二题的人数 = 28 - 20 = 8人

答案：A

容斥最值问题

例题3：容斥最值应用

题目：某班级55名同学参加语文、数学二门课的考试。已知语文51人及格，数学48人及格，则只有语文一门课程及格的人数最多有（ ）人。

  • A. 3
  • B. 4
  • C. 7
  • D. 8

解析：

只有语文一门课程及格的人数 = 语文及格人数 - 语文数学都及格人数 = 51 - 语文数学都及格人数

想要只有语文一门课程及格的人数尽量多，则需要语文数学都及格人数尽量少。

而 A∩B=A+B−A∪B=51+48−A∪B=99−A∪BA \cap B = A + B - A \cup B = 51 + 48 - A \cup B = 99 - A \cup B

想要A∩BA \cap B尽量少，则需要A∪BA \cup B尽量多，A∪BA \cup B最多为全班55人

所以 A∩BA \cap B 最少为 99 - 55 = 44人

所以只有语文一门及格的人数最多可以有 51 - 44 = 7人

答案：C

重要公式：A+B−全集合≤A∩B≤min⁡(A,B)A + B - \text{全集合} \leq A \cap B \leq \min(A, B)

二、三集合容斥

基本原理

三集合容斥原理：

  • A+B+C(总人次)=一层+二层+三层A + B + C(\text{总人次}) = \text{一层} + \text{二层} + \text{三层}
  • A+B+C(总人次)=仅一层+2×仅二层+3×三层A + B + C(\text{总人次}) = \text{仅一层} + 2 \times \text{仅二层} + 3 \times \text{三层}
  • A+B+C(总人次)=一层+仅二层+2×三层A + B + C(\text{总人次}) = \text{一层} + \text{仅二层} + 2 \times \text{三层}

标准公式：

  • 总人数=A+B+C−(A∩B+A∩C+B∩C)+A∩B∩C\text{总人数} = A + B + C - (A \cap B + A \cap C + B \cap C) + A \cap B \cap C
  • 总人数=A+B+C−仅二层−2×三层\text{总人数} = A + B + C - \text{仅二层} - 2 \times \text{三层}

例题4：三集合容斥基础应用

题目：某旅行团共有48名游客，都报名参观了三个景点中的至少一个。其中，只参观了一个景点的人数与至少参观了两个景点的人数相同，是参观了三个景点的人数的4倍。则需要为这些游客购买多少张景点门票：

  • A. 48
  • B. 72
  • C. 78
  • D. 84

解析：

假设只参观了一个景点的人数为a，只参观了两个景点的人数为b，参观了三个景点的人数为c。

根据题意：

  • a+b+c=48a + b + c = 48
  • a=b+ca = b + c（只参观一个景点的人数 = 至少参观两个景点的人数）
  • a=4ca = 4c（只参观一个景点的人数是参观三个景点人数的4倍）

由 a=b+ca = b + c 和 a+b+c=48a + b + c = 48，可得 a=b+c=24a = b + c = 24

由 a=4ca = 4c，可得 c=24÷4=6c = 24 \div 4 = 6

所以 b=24−6=18b = 24 - 6 = 18

一共需要购买门票数 = 24+18×2+6×3=24+36+18=7824 + 18\times2 + 6\times3 = 24 + 36 + 18 = 78张

答案：C

例题5：三集合容斥应用

题目：为了解某校乒乓球、篮球、排球三种球类的运动情况，采访了某班的同学，了解到会打乒乓球的32人，会打篮球的25人，会打排球的23人，只会打两种球类的18人，三种球类都会打的8人，三种球类都不会的6人，问这个班共有多少人？

  • A. 50
  • B. 52
  • C. 60
  • D. 76

解析：

根据三集合公式：总人数=A+B+C−仅二层−2×三层\text{总人数} = A + B + C - \text{仅二层} - 2 \times \text{三层}

会打球的总人数 = 32+25+23−18−2×8=80−34=4632 + 25 + 23 - 18 - 2\times8 = 80 - 34 = 46人

所以共有 46+6=5246 + 6 = 52人

答案：B

例题6：问卷调查容斥问题

题目：某高校做有关碎片化学习的问卷调查，问卷回收率为90%，在调查对象中有180人会利用网络课程进行学习，200人利用书本进行学习，100人利用移动设备进行碎片化学习，同时使用三种方式学习的有50人，同时使用两种方式学习的有20人，不存在三种方式学习都不用的人。那么，这次共发放了多少份问卷？

  • A. 370
  • B. 380
  • C. 390
  • D. 400

解析：

回收问卷人数 = 180+200+100−20−50×2=360180 + 200 + 100 - 20 - 50\times2 = 360人

所以发放问卷数 = 360÷0.9=400360 \div 0.9 = 400人

答案：D

例题7：选修课容斥问题

题目：某专业有学生50人，现开设有甲、乙、丙三门选修课。有40人选修甲课程，36人选修乙课程，30人选修丙课程，兼选甲、乙两门课程的有28人，兼选甲、丙两门课程的有26人，兼选乙、丙两门课程的有24人，甲、乙、丙三门课程均选的有20人。问三门课程均未选的有多少人？

  • A. 1人
  • B. 2人
  • C. 3人
  • D. 4人

解析：

选修甲或乙或丙课程的总人数 = 40+36+30−28−26−24+20=4840 + 36 + 30 - 28 - 26 - 24 + 20 = 48人

所以三门课程均未选的有 50−48=250 - 48 = 2人

答案：B

例题8：岗位胜任容斥问题

题目：某单位26人需要安排在ABC三种不同工作岗位上，发现不能胜任A岗位的有3人，不能胜任B岗位的有2人，不能胜任C岗位的有1人，其中，不能胜任两个及以上岗位的2人，三个岗位都不能胜任的1人，该单位多少人能够胜任所有岗位工作？

  • A. 21
  • B. 22
  • C. 23
  • D. 24

解析：

不能胜任A或B或C岗位的总人数 = 3+2+1−2−1=33 + 2 + 1 - 2 - 1 = 3人

所以能胜任ABC所有岗位的人数 = 26−3=2326 - 3 = 23人

答案：C

例题9：志愿者活动容斥问题

题目：某社区组织35名志愿者参加志愿活动。其中，志愿者可以从楼道巡逻、帮扶空巢老人、扫雪中任选至多2项，参加楼道巡逻、帮扶空巢老人、扫雪的人数分别是16人、23人、24人。其中，楼道巡逻、帮扶空巢老人都参加的有11人，楼道巡逻、扫雪都参加的有9人，则帮扶空巢老人、扫雪都参加的有()人。

  • A. 43
  • B. 12
  • C. 8
  • D. 9

解析：

假设帮扶空巢老人、扫雪都参加的有x人，因为3项任务都参加人数为0

则 35=16+23+24−11−9−x+035 = 16 + 23 + 24 - 11 - 9 - x + 0

x=43−35=8x = 43 - 35 = 8

所以帮扶空巢老人、扫雪都参加的有8人

答案：C

例题10：趣味运动会容斥问题

题目：某单位举办设有A、B、C三个项目的趣味运动会，每位员工三个项目都可以报名参加。经统计，共有72名员工报名，其中参加A、B、C三个项目的人数分别为26、32、38，三个项目都参加的有4人，则仅参加一个项目的员工人数是？

  • A. 48
  • B. 40
  • C. 52
  • D. 44

解析：

总人次 = 26+32+38=9626 + 32 + 38 = 96人次

假设仅参加2个项目人数为x，则 x×(2−1)+4×(3−1)=96−72=24x \times (2-1) + 4 \times (3-1) = 96 - 72 = 24

x=16x = 16

所以仅参加一个项目的员工人数 = 72−16−4=5272 - 16 - 4 = 52人

答案：C

三、容斥最值问题

最少重叠问题

例题11：最少重叠人数

题目：有100人参加运动会的三个比赛项目，每人至少参加一项，其中未参加跳远的有50人，未参加跳高的有60人，未参加赛跑的有70人，问至少有多少人参加了不止一个项目？

  • A. 7人
  • B. 10人
  • C. 15人
  • D. 20人

解析：

参加项目总人次 = (100−50)+(100−60)+(100−70)=120(100-50) + (100-60) + (100-70) = 120人次

现有100人员，要让超过一层人数尽量少，则先铺满一层，还剩 120−100=20120 - 100 = 20人次

多出来的人次尽量堆至最高3层，所以会有至少 20÷(3−1)=1020 \div (3-1) = 10人参加了不止一个项目

答案：B

最多未参与问题

例题12：最多未参与人数

题目：一个班级组织跑步比赛，共设100米、200米、400米三个项目。班级有50人，报名参加100米比赛的有27人，参加200米比赛的有25人，参加400米比赛的有21人。如果每人最多只能报名参加2项比赛，那么该班最多有多少人未报名参赛？

  • A. 11
  • B. 12
  • C. 13
  • D. 14

解析：

总人次 = 27+25+21=7327 + 25 + 21 = 73人次

先要让未报名人数尽量多，则需要让报名参赛人数尽量少

每人最多2项，73 ÷ 2 = 36.5，所以参赛人数至少为37人

所以最多有 50−37=1350 - 37 = 13人未报名参赛

答案：C

例题13：特殊情况处理

题目：一个班级组织跑步比赛，共设100米、200米、400米三个项目。班级有50人，报名参加100米比赛的有38人，参加200米比赛的有14人，参加400米比赛的有20人。如果每人最多只能报名参加2项比赛，那么该班最多有多少人未报名参赛？

  • A. 11
  • B. 12
  • C. 13
  • D. 14

解析：

总人次 = 38+14+20=7238 + 14 + 20 = 72人次

先要让未报名人数尽量多，则需要让报名参赛人数尽量少

因为 38>14+2038 > 14 + 20，所以72人次不可能所有人都参赛两种

最多 14+20=3414 + 20 = 34人参赛2种，此时还剩 72−34×2=472 - 34\times2 = 4人次

所以至少 34+4=3834 + 4 = 38人次参赛，则最多有 50−38=1250 - 38 = 12人未报名参赛

答案：B

注意点：当 A > B + C 时，不能直接除2

最少共同问题

例题14：最少共同借阅

题目：阅览室有100本杂志。小赵借阅过其中75本，小王借阅过70本，小刘借阅过60本，则三人共同借阅过的杂志最少有( )本。

  • A. 5
  • B. 10
  • C. 15
  • D. 30

解析：

总人次 = 75+70+60=20575 + 70 + 60 = 205人次

要让三层尽量低，则一、二层尽量铺满，还剩 205−200=5205 - 200 = 5人次

这5人次只能在第三层铺一层，所以至少有5本是三人共同借阅过的

答案：A

真题扩展

题目：（2024 江苏）某基层工会共有 180 名会员，举行甲、乙两项工会活动，60%的会员参加甲活动，50%的会员参加乙活动，若只参加甲活动的会员有 80 人，则只参加乙活动的会员有( )

  • A.10 人
  • B.28 人
  • C.62 人
  • D.90 人

解析：

解析（两集合容斥）

总人数 180180。

参加甲：60%⇒∣A∣=0.6×180=10860\%\Rightarrow |A|=0.6\times180=108；

参加乙：50%⇒∣B∣=9050\%\Rightarrow |B|=90。 已知“只参加甲”为 80 人，

则交集人数： ∣A∩B∣=∣A∣−只甲=108−80=28.|A\cap B|=|A|-\text{只甲}=108-80=28.

于是“只参加乙”： 只乙=∣B∣−∣A∩B∣=90−28=62.\text{只乙}=|B|-|A\cap B|=90-28=62.

答案：C. 62 人

例（2021 四川）为实现产业振兴，农科院对某县的所有自然村进行了调研，结果发现，适合 种植 A 作物的自然村占4/13。适合种植 B 作物的自然村有 25 个，同时适合种植两种作物的自然村占总数的 1/14，则在该县，不适合种植两种作物的自然村至少有多少个?

  • A.57
  • B.67
  • C.114
  • D.134

解析：

  1. 设总自然村数为 N=182tN=182t（因 413\tfrac{4}{13} 与 114\tfrac{1}{14} 要为整数）。

  2. 则各数为：

  • 适合 A：∣A∣=413N=56t|A|=\tfrac{4}{13}N=56t
  • 适合 B：∣B∣=25|B|=25（题给定值）
  • 同时适合两种：∣A∩B∣=114N=13t|A\cap B|=\tfrac{1}{14}N=13t

  1. “不适合两种”（既不 A 也不 B）为 N−∣A∪B∣=N−(∣A∣+∣B∣−∣A∩B∣)=182t−(56t+25−13t)=139t−25.N-|A\cup B|=N-(|A|+|B|-|A\cap B|)=182t-(56t+25-13t)=139t-25.

  2. 约束与取最小：

  • 必须有 ∣A∩B∣=13t≤∣B∣=25⇒t≤1.|A\cap B|=13t\le |B|=25\Rightarrow t\le 1.
  • 且 tt 为正整数，故唯一可行最小为 t=1t=1。
  1. 代回得最小值：139×1−25=114.139\times1-25=114.

结论：不适合两种作物的自然村至少 114 个（选 C）。

例（2018 山东选调）某高校举办春季运动会，共有 1000 名学生报名参加竞赛项目。为从运动员中选拔人员参加开幕式和闭幕式队列，现把所有运动员从 1 到 1000 进行编号，选出编号为3的倍数的运动员参加开幕式队列，而编号为7的倍数的运动员参加闭幕式队列。问：既不参加开幕式队列也不参加闭幕式队列的运动员有多少人？

  • A.428
  • B.475
  • C.525
  • D.572

解析（倍数计数 + 容斥）

设

  • AA：编号为 3 的倍数（开幕式），∣A∣=⌊10003⌋=333|A|=\left\lfloor\frac{1000}{3}\right\rfloor=333；
  • BB：编号为 7 的倍数（闭幕式），∣B∣=⌊10007⌋=142|B|=\left\lfloor\frac{1000}{7}\right\rfloor=142；
  • 交集为 21 的倍数，∣A∩B∣=⌊100021⌋=47|A\cap B|=\left\lfloor\frac{1000}{21}\right\rfloor=47。

参加至少一个队列的人数：∣A∪B∣=∣A∣+∣B∣−∣A∩B∣=333+142−47=428.|A\cup B|=|A|+|B|-|A\cap B|=333+142-47=428. 既不参加两队列的人数：1000−428=572.1000-428=572.

答案：D. 572

溶液问题中的线段法最值问题