数量关系 第十三课 立体几何

一、基础公式

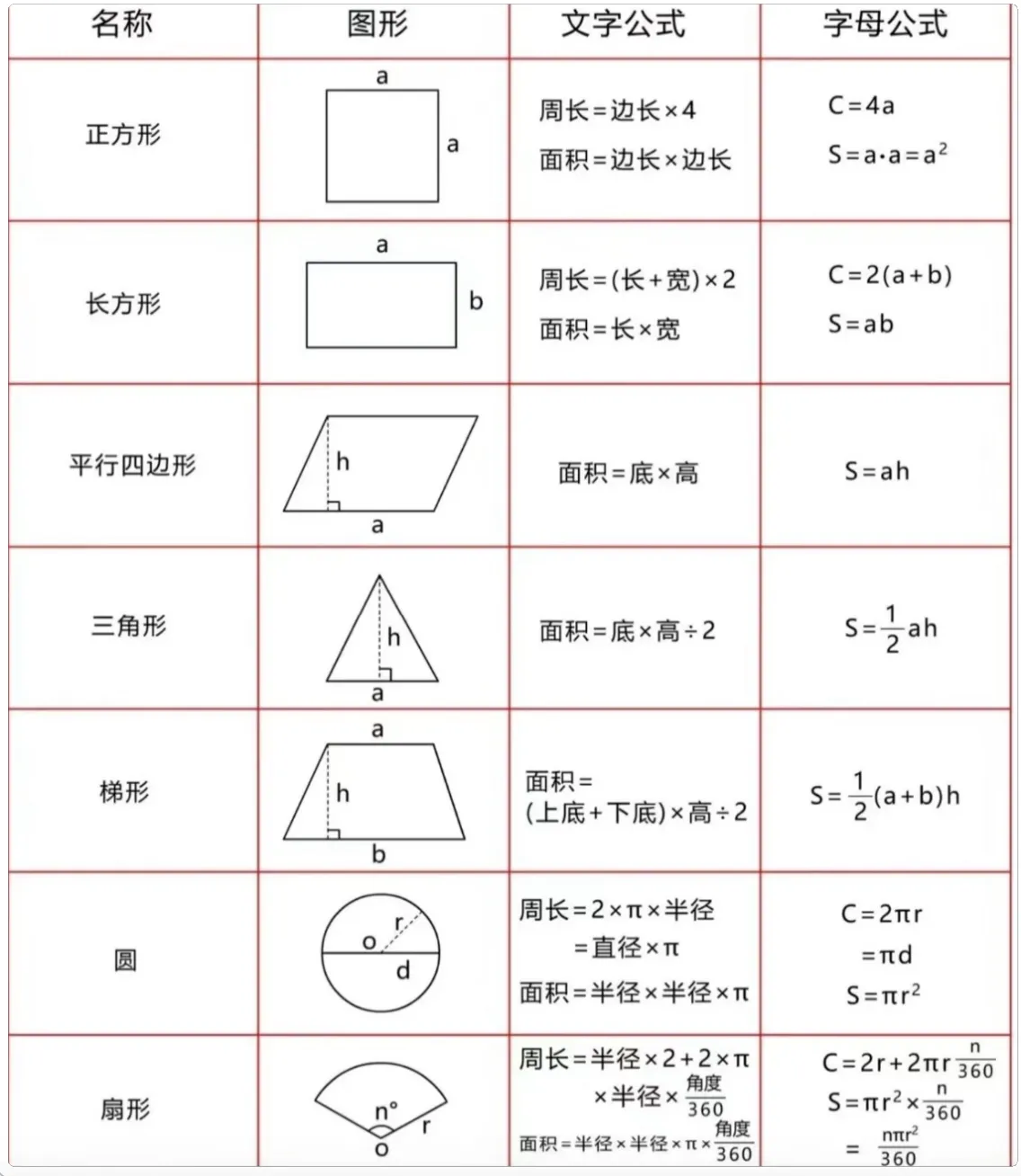
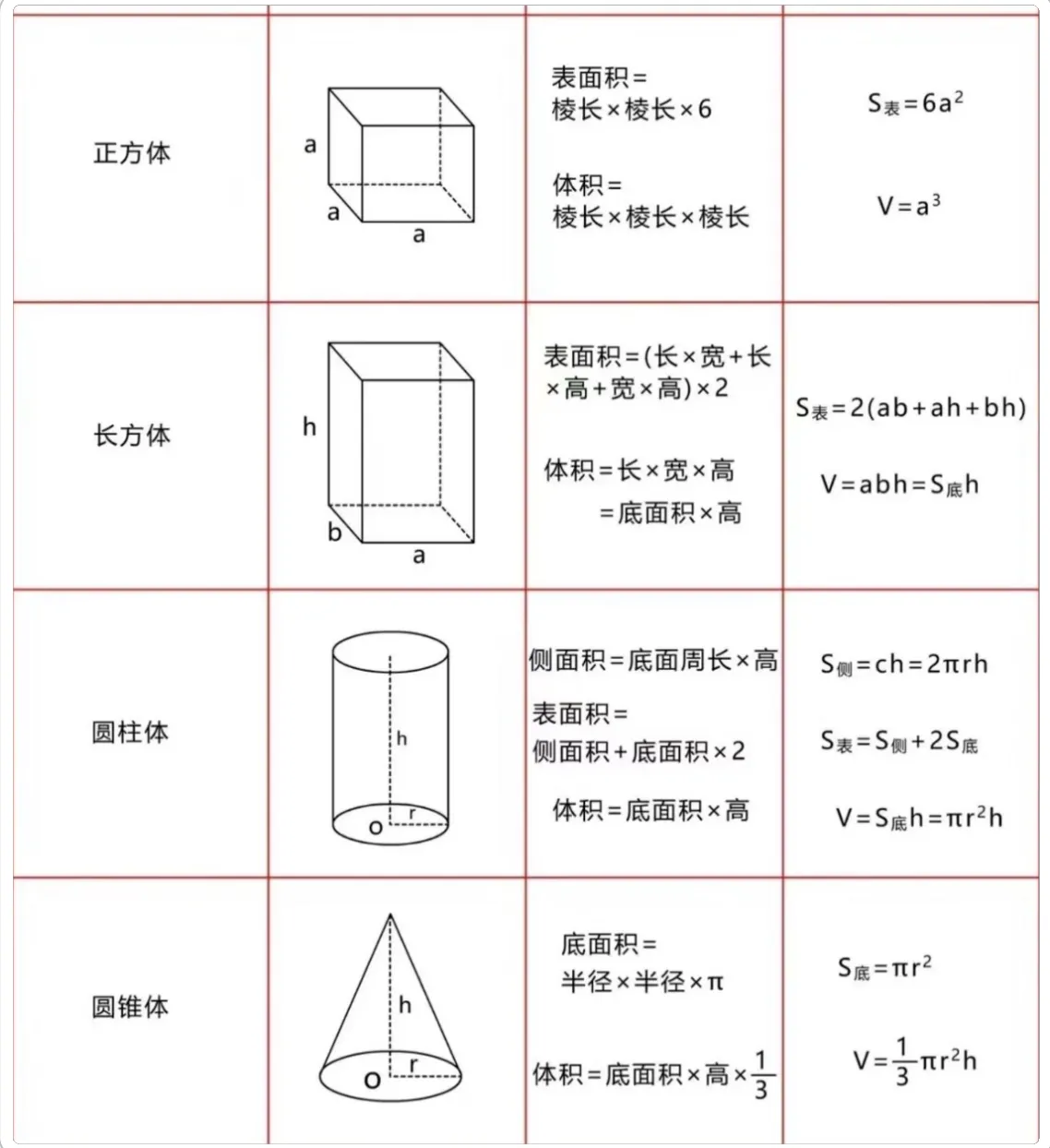
常用体积公式

• 柱体: $V = Sh$
• 棱体: $V = \frac{1}{3}Sh$
• 球体: $V = \frac{4}{3}\pi r^{3} = \frac{1}{6}\pi D^{3}$
• 台体: $V = \frac{1}{3}(S_{1} + S_{2} + \sqrt{S_{1}\times S_{2}})h$

常用表面积公式

• 正方体: $A = 6a^{2}$
• 长方体: $A = 2(ab+bc+ac)$
• 球体: $A = 4\pi r^{2} = \pi D^{2}$
• 圆柱: $A = 2\pi r^{2} + 2\pi rh$
• 圆锥: $A = \pi r^{2} + \pi rl$

几何最值理论

1、立体最值

（1）立体图形中，若表面积一定，越接近于球，体积越大。 （2）立体图形中，若体积一定，越接近于球，表面积越小。

2、平面最值

（1）平面图形中，周长一定，越接近于圆，面积越大； （2）平面图形中，面积一定，越接近于圆，周长越小。

长方形最值（特殊矩形）

（1）四边形周长一定时，正方形面积最大。 （2）四边形面积一定时，正方形周长最小。

二、体积型问题

$\triangle$ 基础计算问题

例 一个体积为125立方厘米的正方体，若它的体积减少98立方厘米，变成新的正方体，则它的表面积减少了（）平方厘米。

A. 58 B. 64 C. 96 D. 98

解析一 因为 $5^{3} = 125$ ，所以原正方体边长为5厘米，表面积 $= 6\times 5^{2} = 150$ 平方厘米。体积减少后 $= 125 - 98 = 27 = 3^{3}$ ，所以新正方体边长为3厘米，表面积 $= 6\times 3^{2} = 54$ 平方厘米。所以减少了 $150 - 54 = 96$ 平方厘米，选 C。

解析二 设正方体原来边长为a厘米，新正方体边长为b厘米，则表面积差 $= 6a^{2} - 6b^{2} = 6(a^{2} - b^{2})$ ，大胆猜测a、b都是整数，结果是6的倍数，选项中只有C符合，所以选 C。

例 有一个长方体容器，长40厘米，宽30厘米，高10厘米，里面的水深6厘米（最大面为底面）。如果把这个容器盖紧，再竖起来（最小面为底面），里面的水深是多少厘米：

A. 15 B. 18 C. 24 D. 30

解析 体积 $=$ 底面积 $\times$ 高，水的体积不变，所以水深与底面积成反比。最大底面积 $= 40\times 30$ ，最小底面积 $= 30\times 10$ ，底面积比为4：1，所以水深比为1：4，所以最小底面积时，水深 $= 6\times 4 = 24$ 厘米，选择 C。

例 两个圆柱形水井，甲井的水深是乙井的一半，水面直径是乙井的2倍，蓄水量为40立方米，问乙井的蓄水量为多少立方米？

A. 20 B. 60 C. 40 D. 80

解析 柱体体积 $=$ 底面积 $\times$ 高，乙井底面积圆的直径是甲的一半，根据相似图形面积比 $=$ 长度比²，所以底面积是甲的 $\frac{1}{4}$ ，而水深是甲的2倍，所以体积是甲的 $\frac{1}{4} \times 2 = \frac{1}{2}$ ，即 $40 \times \frac{1}{2} = 20$ 立方米，所以选择A。

例 连接正方体每个面的中心构成一个正八面体（如下图所示）。已知正方体的边长为6厘米，问正八面体的体积为多少立方厘米？（）

A. $18\sqrt{2}$ B. $24\sqrt{2}$ C. 36 D. 72

解析 正八面体看作上下两个四棱锥。锥体体积 $= \frac{1}{3} \times$ 底面积 $\times$ 高，柱体体积 $=$ 底面积 $\times$ 高。图中锥体底面积是柱体的 $\frac{1}{2}$ ，高相同，所以体积是柱体的 $\frac{1}{3} \times \frac{1}{2} = \frac{1}{6}$ 。所以正八面体体积 $= \frac{1}{6} \times 6^3 = 36$ 立方厘米，所以选C。

例 有两种容器，一种为半球形（A），一种为圆锥形（B），其开口圆的直径与高的尺寸如图所示（单位：cm）。若A容器中装满的实验液需要分装到若干个B容器中，则至少需要B容器（）个。

A. 3 B. 4 C. 6 D. 8

解析 A容器体积 $= \frac{1}{2}\times \frac{4}{3}\times \pi \times 10^{3}$ ，B容器体积 $= \frac{1}{3}\times \pi \times 5^{2}\times 10$ ，两者体积比 $= \frac{\frac{1}{2}\times\frac{4}{3}\times\pi\times 10^{3}}{\frac{1}{3}\times\pi\times 5^{2}\times 10} = 8$ 。因此需要8个，选择 D。

立体相似问题

原理

• 相似图形面积比 $=$ 长度比²
• 相似图形体积比 $=$ 长度比³

例 正六面体的表面积增加 $96\%$ ，棱长增加多少？

A. 20% B. 30% C. 40% D. 50%

解析 表面积增加 $96\%$ 即变成1.96倍，所以长度比是 $\sqrt{1.96} = 1.4$ 倍，所以棱长增加 $40\%$ ，选择C。

例 某餐馆承诺25分钟内上齐一桌菜，若超时则未上的菜品免单。每张餐桌上都有一个装满后正好25分钟漏完的圆锥形沙漏（如下图所示）。某位顾客在等待的过程中发现沙漏内上方沙子的高度为原先的一半此时还差一道菜未上，则再过多久还未上菜，这位顾客将享受免单服务？

A. 不到3分钟 B. 3-4分钟 C. 4-5分钟 D. 超过6分钟

解析 大小圆锥形状相似，大圆锥高度是小圆锥高度的2倍，所以体积比 $=$ 长度比³ $= 2^3 = 8$ 倍，所以此时沙子体积代表的时间 $= 25\times \frac{1}{8} = 3.125$ 分钟，所以选择B。

例 某甜品店出售一种规则球形的甜品，该甜品由内部中空的球形面皮（每立方厘米成本0.4元），和实心的芝士球（每立方厘米成本1元）组成，无论甜品大小规格如何，其中的芝士球半径始终为甜品半径的四分之三，已知制作半径为1厘米的该甜品成本约为2.73元，那么要制作半径为2厘米的该甜品，成本约为：

A. 5.46元 B. 7.45元 C. 14.92元 D. 21.84元

解析 由于无论甜品大小规格如何，其中的芝士球半径始终为甜品半径的四分之三，所以大小芝士球属于相似图形，体积比 $=$ 长度比³ $= 2^3 = 8$ 倍，则成本 $= 2.73\times 8 = 21.84$ 元，所以选择D。

例 人工湖的湖面上有一个露出水面3米的圆锥体人工景观（底面朝下）。如人工湖水深减少 $20\%$ ，则该景观露出水面部分的体积将增加 $\frac{61}{64}$ 。问原来的人工湖水深为多少米？

A. 3.5 B. 3.75 C. 4.25 D. 4.5

解析 水深减少，露出水面部分圆锥体积变大，变成 $1 + \frac{61}{64}$ 即 $\frac{125}{64}$ 倍，即长度比变成 $\sqrt[3]{\frac{125}{64}} = \frac{5}{4}$ 倍，即露出水面部分高度增加 $3\times \frac{1}{4} = 0.75$ 米，而这部分高度 $=$ 水深减少高度，所以原来水深 $= 0.75\div 20\% = 3.75$ 米，选择B。

三、面积型问题

表面积计算

例 在一个正方体木块朝上的一面上竖直挖个贯通的正方形通道，已知正方体的边长为 $20cm$ ，通道洞口的边长为 $10cm$ ，则正方体的表面积增加了（ ） $cm^2$ 。

A. 100 B. 400 C. 500 D. 600

解析 增加了4个贯通面的表面积，减少了顶面、底面一部分面积，所以表面积总共增加了 $4\times 10\times 20 - 2\times 10\times 10 = 800 - 200 = 600cm^2$ ，选择D。

例 一个长方体，若高减少3厘米，则成为一个正方体，这时表面积比原来减少了96平方厘米，原来长方体体积是（ ）立方厘米。

A. 384 B. 480 C. 704 D. 4864

解析 假设正方体边长为a，则减少的表面积是一圈侧面积即 $4a\times 3 = 12a = 96$ ，所以 $a = 8$ ，所以原来长方体是长宽为 $8cm$ ，高为 $8 + 3 = 11cm$ 的长方体，体积 $= 8\times 8\times 11 = 704$ 立方厘米，选择C。

例 将一个表面积为18平方厘米的正方体沿对角线切成两块对称的三棱柱（见下图），并将这两块三棱柱重新拼接成一个大的三棱柱。则这个大三棱柱的表面积最大为多少平方厘米？

A. $12 + 2\sqrt{3}$ B. $12 + 6\sqrt{2}$ C. $15 + 2\sqrt{3}$ D. $15 + 6\sqrt{2}$

解析 表面积18，所以正方体边长 $= \sqrt{3}$ ，切开面面积 $= \sqrt{3}\times \sqrt{6} = 3\sqrt{2}$ ，切开后两块对称的三棱柱表面积之和固定 $= 18 + 2\times 3\sqrt{2} = 18 + 6\sqrt{2}$ ，拼成大三棱柱后表面积会减少2个重叠面的面积，所以要想表面积最大，则重叠面应尽量小。切开后三棱锥最小面为三角形面，所以表面积最大三棱柱是把两个小三棱柱的三角面堆叠重合后形成，表面积 $= 18 + 6\sqrt{2} - 3 = 15 + 6\sqrt{2}$ ，选择D。

例 一实心圆锥体的底面半径为r，母线长为 $2r$ 。若截圆锥体得到两个同样的锥体（如图），则所得两个锥体的表面积之和与原圆锥体表面积的比值是？

A. $\frac{1}{2}$ B. $\frac{\pi + 4\sqrt{3}}{6}$ C. $\frac{3\pi + 2\sqrt{3}}{3\pi}$ D. $\frac{3\pi + 4}{6\pi}$

解析 分母原表面积必然带 $\pi$ ，后来表面积是增加2个三角形面积，且三角形高 $= \sqrt{3}r$ ，所以分子是 $a\pi + b\sqrt{3}$ 形式，只有选项C符合，选择C。

例 有一正方体模具，边长为10。如图所示，现要以一个面的内接圆为底面，挖掉一个与正方体等高的圆柱体，则剩余模具的表面积为：

A. $100(4 - \frac{\pi}{4})$ B. $100(4 + \frac{\pi}{2})$ C. $100(6 + \frac{\pi}{2})$ D. 600

解析 原正方体表面积 $= 6\times 10\times 10 = 600$ ，贯穿后增加贯穿侧面表面积，减少顶面底面各一个圆面积。贯穿侧面积 $= 2\pi rh = 2\pi \times 5\times 10 = 100\pi$ ，圆面积 $= \pi r^{2} = \pi \times 5\times 5 = 25\pi$ ，所以剩余模具表面积 $= 600 + 100\pi - 2\times 25\pi = 600 + 50\pi = 100(6 + \frac{\pi}{2})$ ，所以选择 C。

解析 剩余模具表面积 $=$ 原正方体表面积 $+$ 贯穿圆柱侧面积 $- 2\times$ 贯穿圆面积 $= 600 - a\pi$ ，只有C、D符合，出题人大概率不会正好让圆柱侧面积与顶部底部圆面积相等，所以选择C。

四、距离型问题

表面展开最短路径

例 如图，有一个圆柱体，它的高为20，底面半径为5．如果一只蚂蚁要从圆柱体下底面的A点，沿圆柱表面爬到与A相对的上底面B点，则蚂蚁爬的最短路线长约为多少（π取3）？

A. 15米 B. 17米 C. 21米 D. 25米

解析 因为圆柱体底面周长 $= 2\pi r = 2\pi \times 5 = 10\pi = 10\times 3 = 30$ ，所以将圆柱体侧面从A处展开，可以得到一个长为30、宽为20的长方形。此时B位于长方形上方中间的位置，则 $AC = 15$ ， $BC = 20$ ，此时AB之间最短路线即AB距离根据勾股定理/勾股数比例可知等于25，所以选择 D。

例 如图，有一个圆柱体，它的高为20，底面半径为5．如果一只蚂蚁要从圆柱体下底面的A点，沿圆柱表面爬到上底面B点（注：绕行，不是直接由A到B），则蚂蚁爬的最短路线长约为 ______(π取3)

A. $15\sqrt{7}$ 米 B. 25米 C. $10\sqrt{13}$ 米 D. 40米

解析 因为圆柱体底面周长 $= 2\pi r = 2\pi \times 5 = 10\pi = 10\times 3 = 30$ ，所以将圆柱体侧面从A处展开，可以得到一个长为30、宽为20的长方形。则 $AC = 30$ ， $BC = 20$ ，此时AB之间最短路线即AB距离根据勾股定理/勾股数比例可知等于 $10\sqrt{13}$ ，所以选择C。

例 如图，圆锥高 $6\sqrt{3}$ 厘米，底面半径为6厘米，一只蚂蚁从A点沿圆锥侧面爬行到B点，则最短的距离为（）厘米。

A. 12 B. 12√2 C. 6π D. 24

解析 将圆锥侧面展开可得到如下图所示扇形。因为扇形半径 $=$ 圆锥母线长，根据勾股定理，高与底面半径比为 $\sqrt{3}:1$ ，所以母线是底面半径2倍即 $12cm$ 。而扇形弧长 $=$ 圆锥底面周长 $= 2\pi \times 6 = 12\pi$ ，而扇形半径完整圆周 $= 2\pi \times 12 = 24\pi$ ，所以扇形角度 $= 360^{\circ}\times \frac{12\pi}{24\pi} = 180^{\circ}$ ，B在A对面即AB是一半弧长，所以 $\angle AOB = 90^{\circ}$ 所以根据勾股定理， $AB = 12\sqrt{2}$ ，而两点之间直线最短，所以最短距离 $= AB = 12\sqrt{2}$ ，选择B。

例 一个长7厘米、宽5厘米、高3厘米的长方体盒子。一只瓢虫从盒子的任意一个顶点，爬到与设定点在同一体对角线的另一个顶点，则所有情形的爬行路线的最小值是：

A. $\sqrt{153}$ B. $\sqrt{109}$ C. $\sqrt{171}$ D. $\sqrt{113}$

解析 如下图所示，瓢虫从A爬到对角线顶点C的最短距离 $= AC'$ ，而 $AC' = \sqrt{AD^{2} + C'D^{2}} = \sqrt{(AB + BD)^{2} + C'D^{2}} = \sqrt{AB^{2} + BD^{2} + 2AB \times BD + C'D^{2}}$ ，而AB、BD、C'D必然由长宽高组成， $AB^2 + BD^2 + C'D^2$ 为定值，所以AC要尽量小，则就是 $AB \times BD$ 尽量小，最小为宽 $\times$ 高。所以AC最小值 $= \sqrt{7^{2} + 5^{2} + 3^{2} + 2\times 3\times 5} = \sqrt{113}$ ，所以选择 D。

五、角度型问题

例 商家门口摆放了一把正四棱锥形（底面为正方形，侧面为四个全等的等腰三角形）的遮阳伞，第一次伞撑开到图1所示的位置，伞柄与伞骨成角 $\angle CPQ$ 为 $30^{\circ}$ ，继续撑开到如图2所示的位置，伞柄与三骨成角 $\angle C'PQ'$ 变为 $60^{\circ}$ ，那么第二次伞撑开后形成的正方形A’B’C’D’是第一次撑开后正方形ABCD面积的：

图1

图2

A. $3\sqrt{2}$ 倍 B. $\sqrt{3}$ 倍 C. 2倍 D. 3倍

解析 相似图形面积比 $=$ 长度比²，所以我们关注底部正方形内长度的变化。而前后伞形变化是由于打开角度不同引起，图 $1\angle CPQ$ 为 $30^{\circ}$ ，所以 $CQ = CP\times \sin 30^{\circ} = \frac{1}{2}CP$ ；图 $2\angle C'PQ'$ 变为 $60^{\circ}$ ，所以 $C'Q' = CP\times \sin 60^{\circ} = \frac{\sqrt{3}}{2}CP$ ，而CQ、C’Q’都是底面正方形的一半对角线，长度比为 $\sqrt{3}$ ，则面积比为 $(\sqrt{3})^{2} = 3$ 倍，所以选择 D。公众号 樱有尽有

六、球形汉堡问题

原理

构建直角三角形、勾股定理解题

例 如下图，在半径为5厘米的球体上钻一个底面半径是3厘米的圆柱形洞，则洞的内壁面积为（）平方厘米。

A. 36π B. 48π C. 56π D. 72π

解析 圆柱洞内壁面积 $=$ 圆柱侧面积 $= 2\pi rh = \pi \times BC\times AB$ 。根据题意已知圆柱半径为 $3cm$ ，所以 $BC = 3cm\times 2 = 6cm$ ，而AC是球体直径，所以 $AC = 5cm\times 2 = 10cm$ ，所以根据勾股定理 $AB = \sqrt{AC^{2} - BC^{2}} = \sqrt{10^{2} - 6^{2}} = 8cm$ ，所以内壁面积 $= 6\times 8\times \pi = 48\pi$ ，选择 B 。

例 球面上两点之间的最短距离，就是经过两点的大圆在这两点间的一段弧长（大圆就是经过球心的平面截球面所得的圆）。我们将这个弧长叫做两点的球面距离。已知在北纬 $45^{\circ}$ 的纬度圈上有A、B两地，A在东经 $14^{\circ}$ ，B在东经 $104^{\circ}$ ，设地球（近似看做球体）的半径为R，则A、B两地的球面距离是多少？（）

数量关系讲义

A. $\frac{\pi R}{2}$ B. $\frac{\pi R}{3}$ C. $\frac{\pi R}{4}$ D. $\frac{\pi R}{4}$

因为A、B在北纬 $45^{\circ}$ ，所以 $\angle O_1AO = 45^\circ$ $\Delta O_1AO$ 是等角直角三角形，所以 $O_1A = \frac{\sqrt{2}}{2}R$ ，同理解析 $O_1B = \frac{\sqrt{2}}{2}R$ 。因为A在东经 $14^{\circ}$ ，B在东经 $104^{\circ}$ ，所以 $\angle AO_1B = 90^{\circ}$ ， $\Delta AO_1B$ 是等角直角三角形，所以 $AB = \frac{\sqrt{2}}{2}R\times \sqrt{2} = R$ 。则 $AB = AO = BO = R$ ，AOB是等边三角形， $\angle AOB = 60^{\circ}$ ，所以绿色弧 $AB = \frac{60^{\circ}}{360^{\circ}} \times 2\pi R = \frac{\pi R}{3}$ ，所以选择 B 。

注：已知半径算弧长重点在角度关系，而 $\angle AOB$ 大小又主要由AB长度决定，AB越长 $\angle AOB$ 越大，所以要从题干提供的角度关系计算出AB长度再推及 $\angle AOB$ 大小算出弧长。